New article published in Design Issues:
Beyond Affordances: Closing the Generalization Gab between Design and Cognitive Science
Random thoughts about the nature of cognitive systems

Beyond Affordances: Closing the Generalization Gab between Design and Cognitive Science
Peirce introduce Abduction (or Hypothesis) as an alternative to classical forms of rationality (induction, deduction). I contend that this alternative is more typical of everyday reasoning or common sense. And further, that it is a form of rationality that is particularly well suited to both the dynamics of circles and the challenges of complexity. However, my understanding of Abduction may not be representative of how many philosophers or logicians think about it.
In my view, what Peirce was describing is what in more contemporary terms would be described as an adaptive control system, as illustrated in the following figure.This figure represents medical treatment/diagnosis as an adaptive control system. This system has two loops that are coupled.
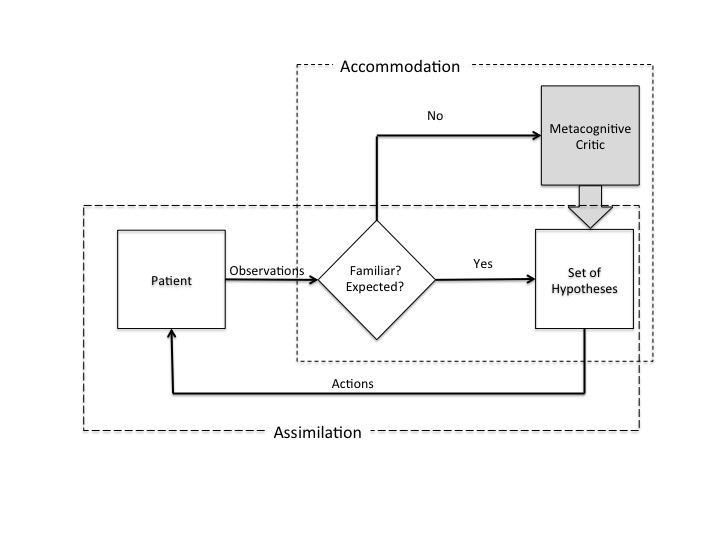
The lower loop is akin to what Piaget described as assimilation or what control theorists would describe as a feedback control system. This system begins by treating the patient based on existing schema (e.g., internal models of typical conditions; or standard procedures). If the consequences of those actions are as expected, then the physician will continue to follow the standard procedures until the 'problem' is resolved. However, if the consequences of following the standard procedures are 'surprising' or 'unexpected' and the standard approaches are not leading to the desired outcomes, then the second loop becomes important.
The upper loop is akin to what Piaget described as accommodation and this is what makes the loop 'adaptive' from the perspective of control theory. Other terms for this loop from cognitive psychology are 'metacognition' and 'situation awareness.'
The primary function of the upper loop is to monitor performance of the lower loop for deviations from expectations. Basically, the function is to evaluate whether the hypotheses guiding actions are appropriate to the situation. Are the physician's internal model or expectations consistent with the patients actual condition? In other words, is the patients condition consistent with the expectations underlying the standard procedures?
If the answer is no, then the function of the upper loop is to alter the hypotheses or hypothesis set to find one that is a better match to the patient's actual condition, In other words, the function of the upper loop is to come up with an alternative to the standard treatment plan. In Piaget's terms, the function is to alter the internal schema guiding action.
The dynamic of the adductive system as illustrated here is very much like what Lindblom described as 'muddling through' or 'incrementalism.' In other words, the logic of this system is trial and error. In facing a situation, decisions and actions are typically guided by generalization from past successes in similar situations (i.e., the initial hypothesis or schema; or standard procedure). If the consequences are as expected, then the schema guiding behavior is confirmed and the experience of the physician is not of decision making or problem solving, but rather it is "just doing my job."
If the consequences of the initial trials are not as expected, then skepticism is raised with respect to the underlying schemas and alternatives will be considered. The physician experiences this as problem solving or decision making - "What is going on here? What do I try next?" This process is continued iteratively until a schema or hypothesis leads to a satisfying outcome.
This dynamic is also akin to natural selection. In this context the upper loop is the source of variation and the lower loop provides the fitness test. The variations (i.e., hypotheses) that lead to success (i.e., good fits), will be retained and will provide the basis for generalizing to future situations. When the ecology changes, then new variations (e.g., new hypotheses or schema) may gain a selective advantage.
Lindblom's term 'incrementalism' reflects the intuition that the process of adjusting the hypothesis set should be somewhat conservative. That is, the adjustments to the hypothesis set should typically be small. In other terms, the system will tend to anchor on hypotheses that have led to success in the past. From a control theoretic perspective this would be a very smart strategy for avoiding instability, especially in risky or highly uncertain environments.
In his 1985 book Surely You're Joking Mr. Feynman, Richard Feynman describes what he calls 'Cargo Cult' Science:
In the South Seas there is a cargo cult of people. During the war they saw airplanes land with lots of good materials, and they want the same thing to happen now. So they've arranged to make things like runways, to put fires along the sides of the runways, to make a wooden hut for a man to sit in, with two wooden pieces on his head like headphones and bars of bamboo sticking out like antennas - he's the controller - and they wait for the airplanes to land. They're doing everything right. The form is perfect. It looks exactly the way it looked before. But it doesn't work. No airplanes land. So I call these things cargo cult science, because they follow all the apparent precepts and forms of scientific investigation, but they're missing something essential, because the planes don't land. (p. 310 - 311)
I often worry that academic psychology is becoming a Cargo Cult Science. Psychologists have mastered the arts of experimental design and statistical inference. They do everything right. The form is perfect. But I don't see many airplanes landing. That is, I see lots of publications of clever paradigmatic experiments, but have difficulty extracting much value from this literature for understanding human experience, particularly in the context of complex work - such as clinical medicine. This vast scientific literature does not seem to generalize in ways that suggest practical ways to improve the quality of human experience.
On the surface, these papers appear to be addressing practical issues associated with cognition (e.g., decision making, trust, team work, etc.), but when I dig a bit deeper I am often disappointed, finding that these phenomenon have been trivialized in ways that make it impossible for me to recognize anything that aligns with my life experiences. Thus, I become quite skeptical that the experiments will generalize in any interesting way to more natural contexts. Often the experiments are clever variations on previous research. The experimental designs provide tight control over variables and minimize confounds. The statistical models are often quite elegant. Yet, ultimately the questions asked are simply uninteresting with no obvious implications for practical applications.
Not everyone seems to be caught in this cult. However, those that choose to explore human performance in more natural settings that are more representative of the realities of everyday cognition are often marginalized within the academy and their work is typically dismissed as applied. For all practical purposes, when an academic psychologist says 'applied science' s/he generally means 'not science at all.'
Perhaps, I have simply gotten old and cynical. But I worry that in the pursuit of getting the form of the experiments to be perfect, the academic field of psychology may have lost sight of the phenomenon of human experience.
In his 1985 book Surely You're Joking Mr. Feynman, Richard Feynman describes what he calls 'Cargo Cult' Science:
In the South Seas there is a cargo cult of people. During the war they saw airplanes land with lots of good materials, and they want the same thing to happen now. So they've arranged to make things like runways, to put fires along the sides of the runways, to make a wooden hut for a man to sit in, with two wooden pieces on his head like headphones and bars of bamboo sticking out like antennas - he's the controller - and they wait for the airplanes to land. They're doing everything right. The form is perfect. It looks exactly the way it looked before. But it doesn't work. No airplanes land. So I call these things cargo cult science, because they follow all the apparent precepts and forms of scientific investigation, but they're missing something essential, because the planes don't land. (p. 310 - 311)
I often worry that academic psychology is becoming a Cargo Cult Science. Psychologists have mastered the arts of experimental design and statistical inference. They do everything right. The form is perfect. But I don't see many airplanes landing. That is, I see lots of publications of clever paradigmatic experiments, but have difficulty extracting much value from this literature for understanding human experience, particularly in the context of complex work - such as clinical medicine. This vast scientific literature does not seem to generalize in ways that suggest practical ways to improve the quality of human experience.
On the surface, these papers appear to be addressing practical issues associated with cognition (e.g., decision making, trust, team work, etc.), but when I dig a bit deeper I am often disappointed, finding that these phenomenon have been trivialized in ways that make it impossible for me to recognize anything that aligns with my life experiences. Thus, I become quite skeptical that the experiments will generalize in any interesting way to more natural contexts. Often the experiments are clever variations on previous research. The experimental designs provide tight control over variables and minimize confounds. The statistical models are often quite elegant. Yet, ultimately the questions asked are simply uninteresting with no obvious implications for practical applications.
Not everyone seems to be caught in this cult. However, those that choose to explore human performance in more natural settings that are more representative of the realities of everyday cognition are often marginalized within the academy and their work is typically dismissed as applied. For all practical purposes, when an academic psychologist says 'applied science' s/he generally means 'not science at all.'
Perhaps, I have simply gotten old and cynical. But I worry that in the pursuit of getting the form of the experiments to be perfect, the academic field of psychology may have lost sight of the phenomenon of human experience.
A new edition of our What Matters? book is now available online.
In the new version an acknowledgment section, endorsements, indexes, and a back cover have been added. Also, a number of typos have been corrected.
The paperback edition is now available for purchase through What Matters on Lulu
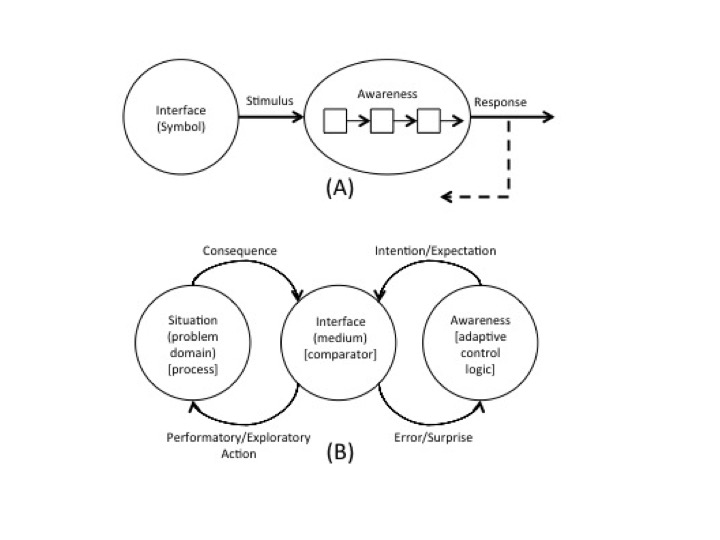
(A) The cognitive system as an open-loop dynamic. (B) The cognitive system as a closed-loop dynamic.
Another very important distinction between how the dyadic and triadic frames for psychology have developed is that the dyadic frame tends to view the cognitive dynamic as an open-loop causal system. In this open-loop perspective, a causal sequence, akin to a sequence of dominos, is typically assumed:
stimuli --> sensations --> perception --> decision --> response.
In this framework, the key is to describe the internal computations (i.e., transfer functions) that translate input to output for each of the distinct stages of information processing. There is, at least an implication, that each of the distinct stages can be understood in isolation from the other stages (e.g., as modules within a computer program); and researchers typically identify with specific stages in this sequence (e.g., one might describe herself as a perceptual researcher, another might call himself a decision researcher, while another might be referred to as a motor control researcher).
In contrast, the triadic frame tends to view the cognitive dynamic as a closed-loop system. In the closed-loop system, the precedence relationships in time that have typically been used to differentiate causes (prior events) from effects (later events) are lost. For example, in the circular system responses can be both causes of stimuli (e.g., looking around) and the effects of stimuli (e.g., orienting to a sound). In a circular system, there is no sense in which any portion of the circle is logically prior to any other portion of the circle. Thus, causal explanations and parsings based on a domino model (based on sequence in time) make no sense for a closed-loop dynamic.
In a closed-loop dynamic there are constraints at the system level (stability) that determine relations that must be satisfied by the components. Thus, for the system to be stable (i.e., to survive) certain relations among the components must be satisfied. Thus, in contrast to the open-loop system where the behavior of the whole is determined by the behavior of the parts. The opposite is true of circular systems - the circular dynamics of the whole (i.e., the organization) creates constraints that the components must satisfy or the system will go out of existence.
For example, in the circular dynamic associated with prey-predator systems, it makes no sense to isolate either the prey or the predator as the cause of the pattern of population levels. Unless certain relations exist between the prey and predators (e.g., as described by a differential equation) the system will either converge on a stable population, oscillate, or collapse into extinction. It is important to emphasize that a differential equation expresses constraints over time associated with relations among the components. The equations describe the coupling of prey and predators. In the dynamic of cognition we are interested in the coupling of perception and action through an ecology.
In the open-loop dynamic, the focus tends to be on events in time and the challenge is to identify the aspects of prior effects that cause later events (e.g., find the root cause of an accident by tracing back in time to find the initiating fault). However, in dealing with closed-loop dynamics explanations tend to be better framed in terms of constraints over time. For example, the laws of motion are constraints over time that are typically expressed in the form of a differential equation. The constraints over time, do not determine events, but they set limits on the fields of possible events. For example, the laws of motion set constraints on the possible trajectories a body might take (e.g., aerodynamics). Similarly, a goal (e.g., to land safely at a specific airport) or value system (e.g., a desire to minimize energy consumption) will not determine the path of an aircraft. However, these constraints will limit the set of possible paths.
The term circular causality has typically been used to indicate that the logic of circular dynamics requires new ways to think about causality and explanation. However, this term does not identify the key distinction from typical causal reasoning. I prefer to say that when dealing with circular systems, it is necessary to dispense with the notion of causality all together and to replace it with the construct of constraint.
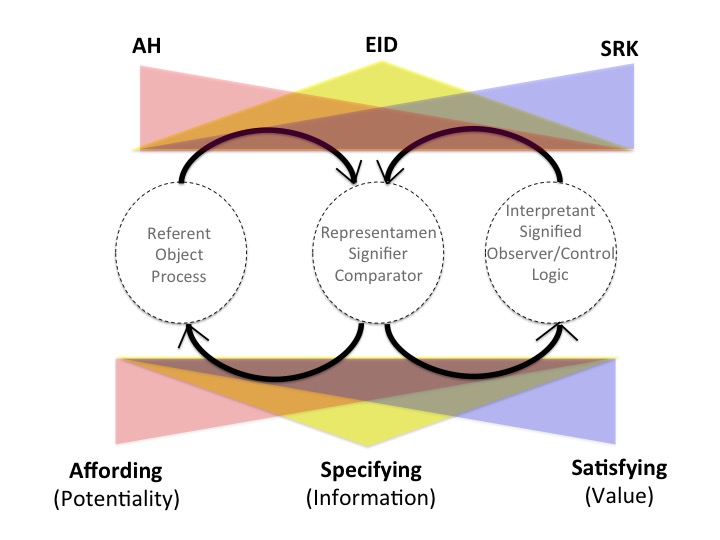
I think this shift has some similarities with the shift from particle based explanations to field based explanations in physics. Thus, rather than framing psychology in terms of discovering the causes of behavior, the focus shifts to understanding the dynamic constraints on behavior. In this context the terms affording, specifying, and satisfying refer to different sources of constraint on the cognitive dynamic. Affording refers to the constraints on action (e.g., laws of motion). Specifying refers to the constraints on information (e.g., laws of optics). Finally, satisfying refers to the constraints on value (e.g., principles of reinforcement and punishment).
The figure below suggests how these three sources of constraint map onto the triadic semiotic. Note that these are constraints over the components of the system, but that tend to be grounded in different components. Affording is grounded in the physics of the ecology (e.g., the nature of the gravitational field, the surfaces of support, vehicle dynamics, etc.). Specifying is grounded in the properties of the interface or representation (e.g., optical flow field, acoustic field, computer interface). Satisfying is grounded in the intentions and preferences of the cognitive agent.
Note that there tends to be a parallel structure in the way in which Rasmussen has framed Cognitive Systems Engineering (CSE). His Abstraction Hierarchy (AH) focuses on how the domain constraints shape the affordances (determine the field of possibilities) relative to the goals and capabilities of an agent. The SRK model tends to reflect the internal strategies and expectations of an agent in terms of Skills, Rules, and Knowledge relative to the problem constraints and the intentions of the agent. Finally, the Ecological Interface Design (EID) focuses on the design of interfaces that specify the field of possibilities in ways that are consistent with the capabilities of an agent. I will talk more about CSE in future blogs. For those interested in going into this deeper, I suggest you look at the link to Bennett & Flach's Interface Design book.
Inspired by the computer metaphor and the developing field of linguistics (e.g., Chomsky), the main stream of cognitive science was framed as a science where mind was considered to be a computational, symbol-processing device that was evaluated relative to the norms of logic and mathematics. However, there were a few, such as James Gibson, who followed a different path.
Gibson followed a path that was originally blazed by functional psychology (e.g., James, Dewey) and pragmatist philosophers (e.g., Peirce). Along this path, psychology was framed in the context of natural selection and the central question was to understand the capacity for humans to intelligently adapt to the demands of survival. Thus, the question was framed in terms of the pragmatic consequences of human thinking (e.g., beliefs) for successful adaptation to the demands of their ecology.
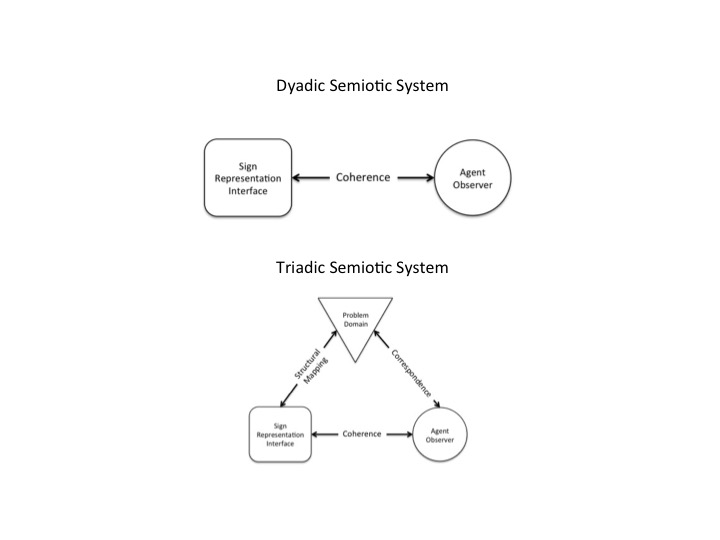
An important foundation for Gibson's ecological approach was Peirce's Triadic Semiotics. In contrast with Saussure's Dyadic approach - Peirce framed the problem of semiotics as a pragmatic problem - rather than as a symbol processing problem. Saussure was impressed by the arbitrariness of signs (e.g., C - A - T) and the ultimate interpretation of an observer (e.g., kind of house pet). In contrast, Peirce was curious about how our interpretation of a sign (e.g., pattern of optical flow) provides the basis for beliefs that support successful action in the world (e.g., braking in time to avoid a collision). In addition to considering the observer's interpretation of the sign, this required a consideration of the relation of the sign to the functional ecology (e.g., how well the pattern specifies relative motion of the observer to obstacles - the field of safe travel), and the ultimate pragmatic consequences of the belief or interpretation relative to adaptations to the ecology (e.g., how skillfully the person controls locomotion).
The figure below illustrates the two views of the semiotic system. In comparing these two systems it is important to keep in mind Peirce's admonition that the triadic system has emergent properties that can never be discover from analyses of any of the component dyads. For Peirce the triad was a fundamental primitive with respect to human experience. Thus, arguing that the whole of human experience is more than the sum of the component dyads.
William 'Bill' Mace provided a clever way to contrast the dyadic framework of conventional approaches to cognition with the triadic framework of ecological approaches to cognition.
The conventional (dyadic) approach frames the question in terms of computational constraints, asking:
How do we see the world the way we do?
The ecological (triadic) approach frames the question in terms of the pragmatic constraints, asking:
How do we see the world the way it is?
For a laboratory science of mind, either framing of the question might lead to interesting discoveries and eventually some of the discoveries may lead to valuable applications. However, for those with a practical bent, who are interested in a cognitive science that provides a foundation for designing quality human experiences, the second question provides a far more productive path. For example, if the goal is to increase safety and efficiency and to support problem solving in complex domains such as healthcare or transportation, then the ecological framing of the question will be preferred! You can't design either training programs or interfaces to improve piloting without some understanding of the dynamics of flight.
If the goal is to discover what matters in terms of skillful adaptations to the demands of complex ecologies, then a triadic semiotic frame is necessary. To understand skill, it is not enough to know what people think (i.e., awareness), it is also necessary to know how that thinking 'fits' relative to success in the ecological context (i.e., the functional demands of situations).
The development of psychology as a science has tended to buy into and to reinforce the dichotomy of mind and matter. In most histories of psychology, Wilhelm Wundt's lab is identified as the first experimental psychology lab - as the birthplace of a scientific psychology. However, certainly there were others who had experimental programs before Wundt (e.g., Fechner and Helmholtz).
Perhaps the reason is that whereas Fechner and Helmholtz were studying relations between mind and matter (i.e., psychophysics), Wundt, with the emphasis on introspection, framed psychology as mental chemistry. This methodology emphasized the distinction between the stimulus as an object in the ecology and the stimulus as a property of mind. And there was a clear understanding that it was only the properties of mind that were of interest to the 'science' of psychology. In fact, Titchener would characterize associations between introspections and the ecological object as 'stimulus errors.' And Ebbinghaus would focus on nonsense syllables in an attempt to isolate the mental chemistry of memory from experiences outside the experimental context.
Of course, not everyone bought into this. William James characterized the experimental work of Wundt and Titchener as 'brass instrument psychology.' In framing a functionalist psychology, James was particularly interested in mind as a capacity for adaptation in relation to the dynamics of natural selection. In this context, the pragmatic relations between mind and matter (satisfying the demands of survival) were a central concern.
Note that Wundt's research program was very broad, particularly if you consider his Volkerpsychologie. Thus, the key point is not to criticize his choice of focus or specialization. Rather, it is the later field of psychology that choses this focus as the 'birthplace' of the science that reinforces the idea that the science of psychology should be framed exclusively in terms of the mind, in isolation from matter (e.g., a physical ecology).
While Behaviorism brought the methodology of introspection under suspicion, and shifted attention to 'behavior,' the idea of 'stimulus' remained psychological (if not mentalistic) in that the nature of the stimulus (e.g., reinforcement versus punishment) was derived from the impact on behavior (e.g., increasing or reducing its likelihood), rather than as a consequence of its physical attributes. Thus, the Laws of learning could be pursued independently from any physical principles (e.g., the Laws of Motion).
With the development of information technologies, the mind again became a legitimate object of study. However, now the topic was not mental chemistry, but mental computation. The computer metaphor added new legitimacy to the separation of mind (i.e., software) from matter (i.e., hardware). And the new science of linguistics, with its basis in a dyadic model of semiotics (Saussure) shifted the focus to symbol processing in a way that made the link between the symbol and the ecology completely arbitrary. The focus was on the internal computations - the rules of grammar, the 'interpretation' that resulted from the mental computations. It became apparent to many that the stimuli for mental computations were arbitrary signs (e.g. C-A-T) and that the 'meanings' of these arbitrary signs were constructed through mental computations.
In this climate, people such as James Gibson, who followed the Functionalist traditions of William James in pursuing the significance of mind for adapting to an ecology, were marginalized. The field of psychology became the study of internal computational mechanisms for processing arbitrary signs. The focus of psychology was to identify the internal constraints of the computational mechanisms. In this context, the most interesting phenomena were errors, illusions, and biases, because these might give hints to the internal constraints of the computations. A mind that was successful or situations where people behaved skillfully tended to be ignored - because the internal constraints were not salient when the mind worked well.
Ironically, in linking mental computations to brain structures, the dichotomy between mind and matter continues to be reinforced, at least to the extent that 'matter' reflects the physical constraints in an ecology. While neuroscience involves the admission that the hardware matters, by isolating the computation to the 'brain' there remains a strong tendency for psychology to ignore the role of other physical properties of the body and ecology in shaping human experience. For many, neuroscience effectively reduces psychology and cognition back to a mental chemistry or to brain mechanisms that can be understood independently from the pragmatic aspects of experience in a complex ecology. In this regard, I fear that increased enthusiasm for neuroscience is a backward step or an obstacle to progress toward a science of human experience.
A division or contrast between two things that are or are represented as being opposed or entirely different. Either/Or
Consisting of two parts, elements, or aspects. Both/And
In Western culture there is a tendency to think about Mind and Matter as dichotomous. That is, mind is considered to be a different kind of thing than matter (e.g. physical bodies). For example, the objects of mind (e.g., ideas) are considered to be massless and are not subject to physical laws (e.g. Laws of Motion). Rather, mental objects are typically associated with the laws of logic or more generally computation (e.g., information theory). This leads to a natural division between the physical sciences (e.g., physics, chemistry, and biology) and the social sciences (e.g., psychology, sociology, economics). Although both groups tend to aspire to similar methodological standards (e.g., well-designed experiments), there is an assumption that the objects of study and the natural laws constraining the behavior of the objects may be fundamentally different kinds of things. This also leads naturally to an assumption that, beyond methodology, there is little that one type of science can learn from the other. That is, there is an implication that each of the two types of sciences can be complete without considering objects of the other type. In other words, there is an assumption that the software can be understood independently from the hardware, and vice versa. The soft sciences study the software and the hard sciences study the hardware.
As the old saw goes: What is mind, never matter. What is matter, never mind.
This view that Mind and Matter are dichotomous is reflected in the parsing of the puzzle shown on the left of the figure below. The challenge for such a perspective is how to address properties of human experience that depend on relationships between mental things (e.g., desires, sensitivity, capability) and physical things (consequences, appearances, physical layout). The challenge is how to add two fundamentally different kinds of things together into a coherent narrative with respect to human experience that reflects properties such as satisfying (e.g., whether a particular type of food will satisfy the desire for healthy nourishment), specifying (e.g., whether a particular pattern in a visual flow field will specify a safe separation from the car ahead of you), or affording (e.g., whether an object requires a one-handed or two-handed grasp).
In fact, one might ask which of the two sciences (i.e., physical or social) owns the phenomenon of human experience? Which science determines whether something is satisfying, whether something is specified, or whether something is afforded? Or do these aspects of experience fall into the gap between the two distinct sciences.
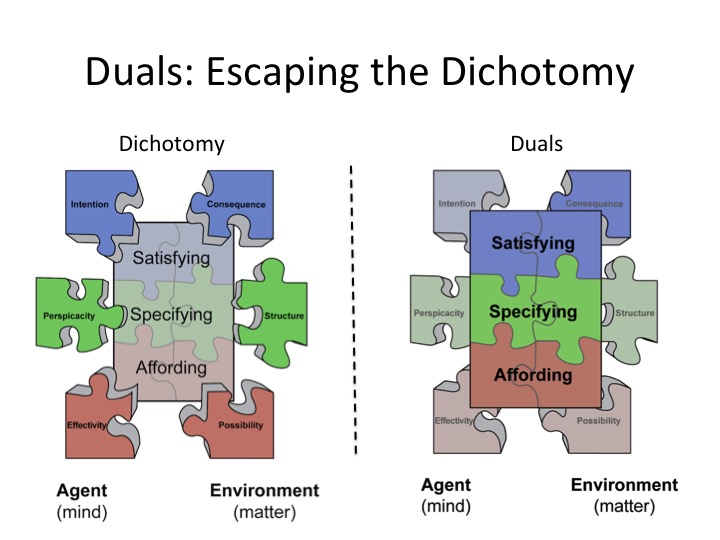
The puzzle diagram on the right suggests a different framework for a single science, where experience is considered to be a joint function of mind and matter. In this perspective, satisfying, specifying, and affording become the objects of study - where these objects are considered to be duals. That is, they reflect relations spanning mind and matter. Thus, each object is ill-defined without specification of both aspects. Thus, the affordance of graspable reflects a relation between the size of an object (e.g., a basketball) and the size of a hand. The specificity depends on a relation between structure in an optical array (e.g., patterns of angular expansion) and an appropriately tuned sensor (e.g., a well-tuned, attentive eye). The satisfying attribute depends on the relation between intentions, needs, or desires (desire for nutrition) and the actual physical consequences (e.g. the digestibility of an object).
The duals of affording, specifying, and satisfying are suggested as the fundamental objects of study for a unified science of experience. These objects are duals in the sense that they refer to relations over mind and matter.
In a recent article on new approaches to designing human experiences, Sanders and Stappers (2008) write "We are heading into a world where experience trumps reality." I think that perhaps William James and Robert Pirsig might suggest something even more drastic. They would perhaps argue that - experience is reality!
This is a major theme developed in our book What Matters. The claim is that the parsing in the left puzzle diagram that treats mind and matter as independent objects of study, breaks human experience into pieces that will never add up to a coherent narrative. On the other hand, we argue that the parsing represented in the right puzzle diagram is a parsing that may be a first step toward a unified science of human experience that spans mind and matter.
A division or contrast between two things that are or are represented as being opposed or entirely different. Either/Or
Consisting of two parts, elements, or aspects. Both/And
In Western culture there is a tendency to think about Mind and Matter as dichotomous. That is, mind is considered to be a different kind of thing than matter (e.g. physical bodies). For example, the objects of mind (e.g., ideas) are considered to be massless and are not subject to physical laws (e.g. Laws of Motion). Rather, mental objects are typically associated with the laws of logic or more generally computation (e.g., information theory). This leads to a natural division between the physical sciences (e.g., physics, chemistry, and biology) and the social sciences (e.g., psychology, sociology, economics). Although both groups tend to aspire to similar methodological standards (e.g., well-designed experiments), there is an assumption that the objects of study and the natural laws constraining the behavior of the objects may be fundamentally different kinds of things. This also leads naturally to an assumption that, beyond methodology, there is little that one type of science can learn from the other. That is, there is an implication that each of the two types of sciences can be complete without considering objects of the other type. In other words, there is an assumption that the software can be understood independently from the hardware, and vice versa. The soft sciences study the software and the hard sciences study the hardware.
As the old saw goes: What is mind, never matter. What is matter, never mind.
This view that Mind and Matter are dichotomous is reflected in the parsing of the puzzle shown on the left of the figure below. The challenge for such a perspective is how to address properties of human experience that depend on relationships between mental things (e.g., desires, sensitivity, capability) and physical things (consequences, appearances, physical layout). The challenge is how to add two fundamentally different kinds of things together into a coherent narrative with respect to human experience that reflects properties such as satisfying (e.g., whether a particular type of food will satisfy the desire for healthy nourishment), specifying (e.g., whether a particular pattern in a visual flow field will specify a safe separation from the car ahead of you), or affording (e.g., whether an object requires a one-handed or two-handed grasp).
In fact, one might ask which of the two sciences (i.e., physical or social) owns the phenomenon of human experience? Which science determines whether something is satisfying, whether something is specified, or whether something is afforded? Or do these aspects of experience fall into the gap between the two distinct sciences.

The puzzle diagram on the right suggests a different framework for a single science, where experience is considered to be a joint function of mind and matter. In this perspective, satisfying, specifying, and affording become the objects of study - where these objects are considered to be duals. That is, they reflect relations spanning mind and matter. Thus, each object is ill-defined without specification of both aspects. Thus, the affordance of graspable reflects a relation between the size of an object (e.g., a basketball) and the size of a hand. The specificity depends on a relation between structure in an optical array (e.g., patterns of angular expansion) and an appropriately tuned sensor (e.g., a well-tuned, attentive eye). The satisfying attribute depends on the relation between intentions, needs, or desires (desire for nutrition) and the actual physical consequences (e.g. the digestibility of an object).
The duals of affording, specifying, and satisfying are suggested as the fundamental objects of study for a unified science of experience. These objects are duals in the sense that they refer to relations over mind and matter.
In a recent article on new approaches to designing human experiences, Sanders and Stappers (2008) write "We are heading into a world where experience trumps reality." I think that perhaps William James and Robert Pirsig might suggest something even more drastic. They would perhaps argue that - experience is reality!
This is a major theme developed in our book What Matters. The claim is that the parsing in the left puzzle diagram that treats mind and matter as independent objects of study, breaks human experience into pieces that will never add up to a coherent narrative. On the other hand, we argue that the parsing represented in the right puzzle diagram is a parsing that may be a first step toward a unified science of human experience that spans mind and matter.