
As I have discussed before, I was introduced to the quantitative methods for analyzing control systems early in my graduate career and it set an important framework for how I have approached Joint Cognitive Systems. Learning mathematical control theory was a struggle for me and I was so eager to share what I learned with other social scientists that I co-authored a book on control theory with Richard Jagacinski who was my major graduate advisor. However, as I began to look at joint cognitive systems that were more complex than the laboratory target acquisition and tracking tasks, I soon realized that every day life is a lot more complex than the laboratory tasks and that the quantitative models that worked for simple servomechanisms and for experimental conditions that required people to act like simple servomechanisms were of limited value.
Everyday life and especially organizational dynamics typically involves many interconnected loops with non-trivial interactions. For example, Boyd's OODA Loop, that is often used to describe skilled behavior, is not a single loop but a multi-loop, adaptive control system.

Joint Cognitive Systems typically have the capacity to learn and to adapt the dynamics of the perception-action coupling to take advantage of that learning. Thus, Joint Cognitive Systems are able to modify or tune the dynamics of the perception-action coupling to fit the unique demands of different situations. The diagram below is one that I developed to show multiple adaptive loops that reflect some of the different strategies that control engineers have used in designing adaptive automatic control systems (e.g., gain scheduling, model-reference adaptive control, self-tuning regulators). Note that the two different styles of arrows reflect different functions - the thin arrows reflect the flow of information that is input to and 'processed' through the dynamics of the different components of the system (i.e., the boxes). However, the block arrows actual operate on the boxes and change or tune the processes within the boxes. For example, in an engineered adaptive control system the result might be to turn down or amp up the sensitivity or 'gain' within a control element. Thus, in adaptive control systems the outer loops typically alter the dynamics of the inner loops.

While the previous figure was designed to imagine skilled motor control as an adaptive system the next diagram was designed based on observations of decision making in the Emergency Department of a major hospital. The point was to illustrate some of the ways in which organizations learn and adapt as a result of experience.

I hope that the preceding diagrams can help readers to get a taste of the complexity of control in the natural world, however I am not fully satisfied with them. I still have a feeling that these diagrams trivialize the real complexity. More recently I have been inspired by the work of Elenor Ostrum on how communities adapt to manage shared resources and to avoid the "tragedy of the commons," and work by the SNAFU catchers (Allspaw, Cook, & Woods) on Dev Ops and managing large internet platforms. It has been suggested that we have to think about layers of control - or polycentric control.
The groups who have actually organized themselves are invisible to those who cannot imagine organization without rules and regulations imposed by a central authority. (Ostrum, 1999, p. 496)
Each technology shift—manual to automated control to multi-layered networks—extends the range of potential control, and in doing so, the joint cognitive system that performs work in context changes as well. For the new joint cognitive system, one then asks the questions of Hollnagel’s test:
What does it mean to be ‘in control’?
How to amplify control within the new range of possibilities? (Woods & Branlat, 2010, p. 101)
The following figure is my attempt to illustrate a polycentric control system. This diagram consists of three layers that seem to have a rough correspondence with Rasmussen's (1986) three levels of cognitive processing (Knowledge-, Rule- and Skill-based) and Thompson's (1967) three means of coordination within organizations (Standardization, Planning, Mutual Adjustment). These levels interact in two distinct ways - one is passing information through direct communication as is typically represented by lines and arrows in standard processing diagrams. However, the second important way is through the propagation of constraints. I am unaware of any convention for diagraming this. In general, higher levels set constraints on the framing of problems at lower levels - in more technical terms - the higher levels impact the degrees of freedom for action at the lower levels. For example, the standards and principles formulated at the highest level set expectations (e.g., through the way people are selected, trained, and rewarded) for the 'proper' way to do planning and the proper way to act. Or the plans, set expectations about responsibilities and actions at the mutual adjustment level. The constraints typically don't specify the actions in detail - but they do shape the framing of situations and often bound the space of possible actions that are considered.
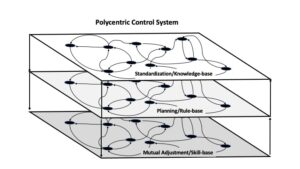
Although it is not possible to model Polycentric Control Systems using the same mathematics that was used to model simple servomechanisms, there are important principles associated with stability that will generalize from the simple systems to the more complex systems. Perhaps, the most significant of these is the impact of time delays on the stability of these systems and the implication for the ability to pick-up patterns and to control or respond to events. The effective time delays associated with communication and feedback will set constraints on the bandwidth of the system. This is seen in models of human tracking as the Crossover Model - in which the effective reaction time sets limits on what frequencies the human can follow without becoming unstable. However, this constraint is also seen almost universally in natural systems in terms of the 1/f characteristic that appears so predominantly when examining performance of many natural systems in the frequency domain. In essence, there are always delays associated with the circulation of information (e.g., feedback) in natural systems and this will always set bandwidth limits on the ability to adapt to situations.
A key attribute of the different layers shown in the diagram of the polycentric control system is that the higher layers will have effective time delays that are progressively longer than the lower layers. On the one hand, this means that high frequency events require the capacity for elements at the mutual adjustment level to be in control (a requirement for subsidiarity). For example, it means that in highly dynamic situations the people on the ground (at the mutual adjustment level) may need to be free to adapt to unexpected situations without waiting for instructions from the higher levels (even if this may require them to deviate from the plan or violate standard operating procedures). On the other hand, this means that higher levels may be better tuned to pick-up patterns that require integration of information over space and time that is outside the bandwidth of people who are immersed in responding to local events (slowly evolving patterns or general principles). Thus, for example an incident command center may be able to provide top-down guidance that allows people at the mutual adjustment level of a distributed organization to coordinate and share resources with people who are outside of their field of regard. Or standard operating procedures are developed and trained to prepare people at the mutual adjustment level to deal efficiently with recurring situations.
So, I hope this short piece has heightened your appreciation for the complexity of natural control systems and wet your appetite to learn more about the dynamics of complex joint cognitive systems. There is a lot more to be said about the nature of polycentric control systems and the implications for the design and management of effective organizations.
